【公式】
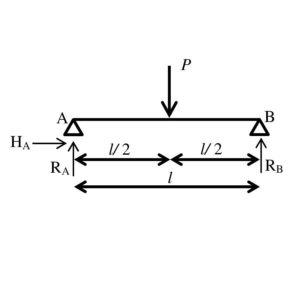
| 反力 | $$R_{A}=R_{B}=P/2$$ |
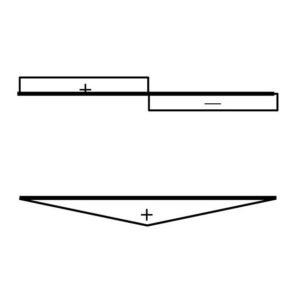
せん断力 $$Q_{max}={P}/{2}$$ 曲げモーメント $$M_{max}={PL}/{4}$$ たわみ量 $$δ_{max}={PL^3}/{48EI}$$
【公式の解法】
1.反力の算定
単純梁は静定構造であるため、力のつり合い式で計算することができます。
X方向の力のつり合い((ΣX=0) )より
$$H_{A}=0$$
Y方向の力のつり合い((ΣY=0))より
$$-P+R_{A}+R_{B} = 0$$
$$R_{A}+R_{B} = Pq …….(1)$$
A点での回転力のつり合い((ΣMA=0))より
$$P ×{L}/{2}-R_{B}× L = 0$$
$$R_{B} = {P}/{2} …….(2)$$
(2)式を(1)式に代入して、\(R_{A}\)を算定します。
$$R_{A}={P}/{2}$$
2.Q,Mの算定
2-1.A点より長さ0~L/2まで
ここからは、梁を長さ\(X_{1}\)で切断した場合の力のつり合いにより、計算していきます。
梁の内部にも軸力、せん断力、曲げモーメントという力が作用しており、これらは外力と釣り合っているのです。
X方向の力のつり合いは、反力の算定で0とわかりましたので省略します。
Y方向の力のつり合い((ΣY=0))より
$$R_{A}-Q = 0$$
$$Q= R_{A}= {P}/{2}$$
A点での回転力のつり合い((ΣMA=0)より
$$Q× X_{1}-M = 0$$
$$M = Q× X_{1}= {PX_{1}}/{2}$$
2-2.A点より、長さL/2~Lまで
計算方法は同様です、次の検討は、外力Pが含まれていることに注意しましょう。
Y方向の力のつり合い((ΣY=0))より
$$R_{A}-P-Q = 0$$
$$Q = P-R_{A}= -{P}/{2}$$
A点での回転力のつり合いより((ΣMA=0)より
$$Q× X_{2}+P ×{L}/{2}-M = 0$$
$$M = {PL}/{2}-QX_{2} = {PL}/{2}+ {P}/{2}× X_{2}$$
$$∴M={P}/{2} × (L-X_{2})$$
Xに特定の距離を入れるとその地点のQとMが算定されます。
基本は支点や最大値を用いることが実務では多いですが、構造力学では、計算問題として、特定の点での応力をもう止めることがあります。
| Xの値 | Q | M |
| 0 | P/2 | 0 |
| L/4 | P/2 | PL/8 |
| L/2 | ±P/2(変曲点) | PL/4(Mmax) |
| 3L/4 | -P/2 | PL/8 |
| L | -P/2 | 0 |
以上。
まとめ
公式が示されているのものは、公式の数値のみを覚えたりしている場合も多いですが、基本に立ち返り成り立ちを把握してみるのもよいのではないでしょうか。




コメント
コメント一覧 (1件)
[…] 単純梁、中央集中荷重の公式とその解法 […]