【公式】片持ち梁　先端集中荷重の公式とその解法

片持ち梁は、一端が固定端、もう一端が自由となっている構造フレームです。

根元部には、曲げモーメントが作用しますので、固定でなければ成り立ちません。

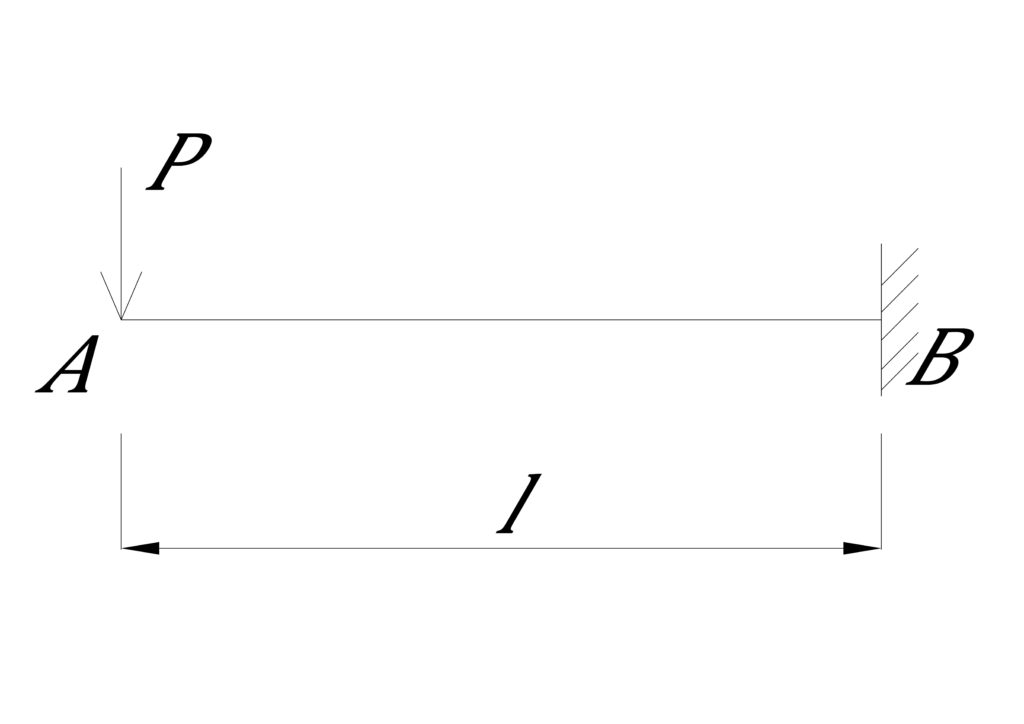
公式

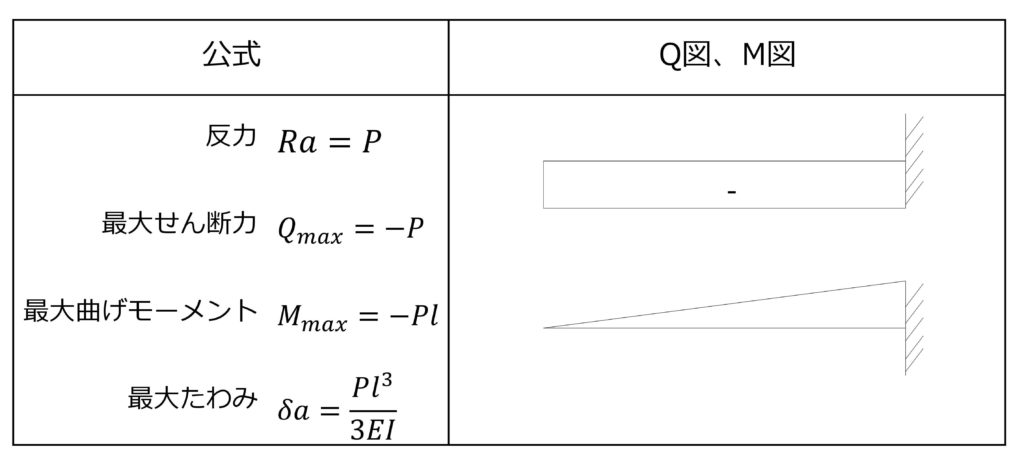
片持ち梁、先端集中荷重の公式は上図のようになります。

この公式を使って、PとLに値を代入していけばいいのですが、今回は、この公式を導くための解法を2章より紹介します。

改訂版 図説 やさしい構造力学

口コミを見る

＼最大7.5%ポイントアップ！／

Amazon

＼ポイント最大11倍！／

楽天市場

Yahooショッピング

ポチップ

公式の解法

片持ち梁は静定構造ですので、力のつり合い式のみで解くことができます。

反力の算定

X方向の力のつり合いより
$$H_{B} = 0$$

Y方向の力のつり合いより
$$-P+V_{B} = 0 $$
$$V_{B} = P $$

B点での曲げモーメントのつり合いより
$$-P / L+M_{B} = 0 $$
$$M_{B} = P × L $$

内部応力の算定

B点から長さxの箇所で部材を切断した場合の力のつり合いより内部応力（Q,M)を算定していきます。

Y方向の力のつり合い
$$Q+V_{B} = 0$$
$$Q = -V_{B}=-P $$

B点での曲げモーメントつり合いより
$$M+M_{B}+Q × x = 0 $$
$$M = -M_{B}-Q × x $$
$$M = -PL+Px $$
$$M = -P(L+x)$$

ここで、x=のとき、
$$M=-PL =M_{max}$$